
レイトレーシングという3Dレンダリング手法があります。
レイ トレーシング(ray tracing, 光線追跡法)は、光線などを追跡することで、ある点において観測される像などをシミュレートする手法である。
あるていど物理法則をシミュレートしていて、 その結果それなりにリアルな画像が出てくるというのが仮想的な世界を作っている感じでテンション上がりますよね。 というわけでいつか作ってみたいと思っていました。
tinyraytracer
256行のC++でレイトレーサを書くという学習用リポジトリがあります。 標準ライブラリの機能のみを使いppm形式の画像を出力するレイトレーサを書いています。
ssloy/tinyraytracer: A brief computer graphics / rendering course
それをもとにDで新世界の神になりました。 こんな感じの画像が出てきます。

kotet/tinyraytracer-d: https://github.com/ssloy/tinyraytracer
300行以上に行数が増えてしまっているように見えます。
しかし実は元のtinyraytracerにはgeometry.hというヘッダファイルがあり、
そこでvec3f等のデータ構造が80行以上かけて実装されているのでこちらも厳密には256行ではありません。
なのでセーフです。
セーフです。
この記事はtinyraytracerのコードと Wiki をパッと読んだだけではわからなかったところを補足する計算ノートです。
球との衝突判定
bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const {
Vec3f L = center - orig;
float tca = L*dir;
float d2 = L*L - tca*tca;
if (d2 > radius*radius) return false;
float thc = sqrtf(radius*radius - d2);
t0 = tca - thc;
float t1 = tca + thc;
if (t0 < 0) t0 = t1;
if (t0 < 0) return false;
return true;
}
t0にはレイの起点から衝突地点までの距離が入ります。
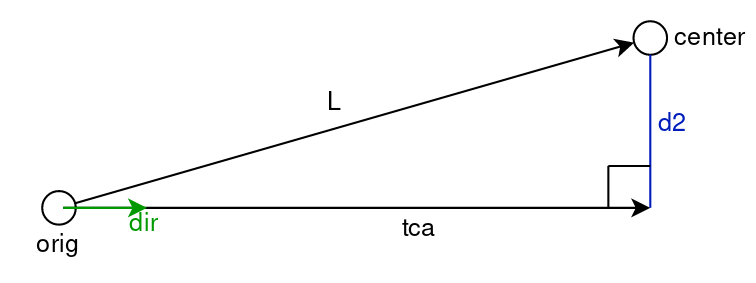
$\vec{L}$と$\vec{dir}$の角度を$\theta$と置く。
$$ tca = \vec{L} \cdot \vec{dir} = |\vec{L}|\cos{\theta} $$
$$ \begin{align} d_2 &= \vec{L} \cdot \vec{L} - tca^2 \\\ &= |\vec{L}|^2 - |\vec{L}|^2\cos^2{\theta} \\\ &= |\vec{L}|^2(1 - \cos^2{\theta}) \\\ &= (|\vec{L}|\sin{\theta})^2 \end{align} $$
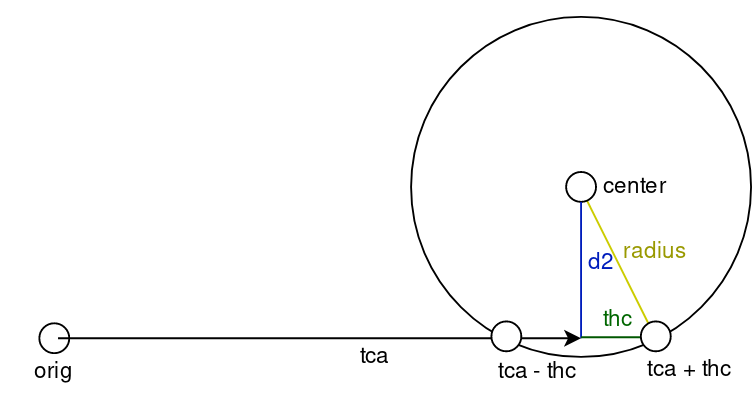
$$ thc = \sqrt{radius^2 - d_2^2} $$
スクリーン座標からの変換
#pragma omp parallel for
for (size_t j = 0; j<height; j++) {
for (size_t i = 0; i<width; i++) {
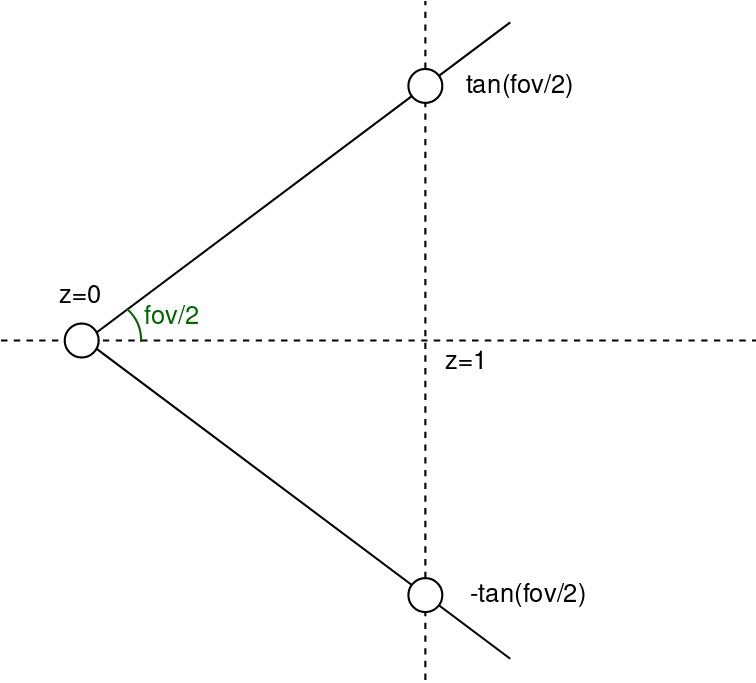
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height;
float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
Vec3f dir = Vec3f(x, y, -1).normalize();
framebuffer[i+j*width] = cast_ray(Vec3f(0,0,0), dir, sphere);
}
}
$$ \frac{1}{width} - 1 \lt \frac{2(i+0.5)}{width} - 1 \lt 1 - \frac{1}{width} $$ $$ (0 \leq i \lt width) $$
反射
Vec3f reflect(const Vec3f &I, const Vec3f &N) {
return I - N*2.f*(I*N);
}
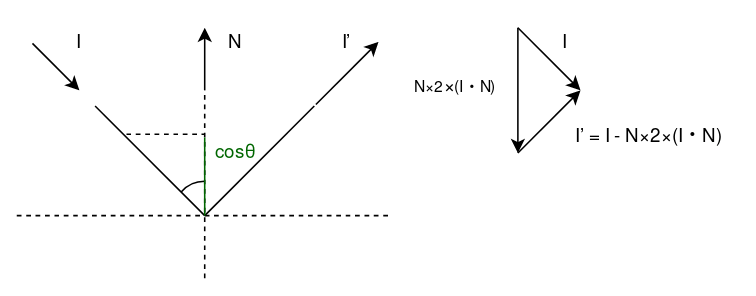
$$ I \cdot N = -\cos{\theta} $$
屈折
Vec3f refract(const Vec3f &I, const Vec3f &N, const float &refractive_index) { // Snell's law
float cosi = - std::max(-1.f, std::min(1.f, I*N));
float etai = 1, etat = refractive_index;
Vec3f n = N;
if (cosi < 0) { // if the ray is inside the object, swap the indices and invert the normal to get the correct result
cosi = -cosi;
std::swap(etai, etat); n = -N;
}
float eta = etai / etat;
float k = 1 - eta*eta*(1 - cosi*cosi);
return k < 0 ? Vec3f(0,0,0) : I*eta + n*(eta * cosi - sqrtf(k));
}
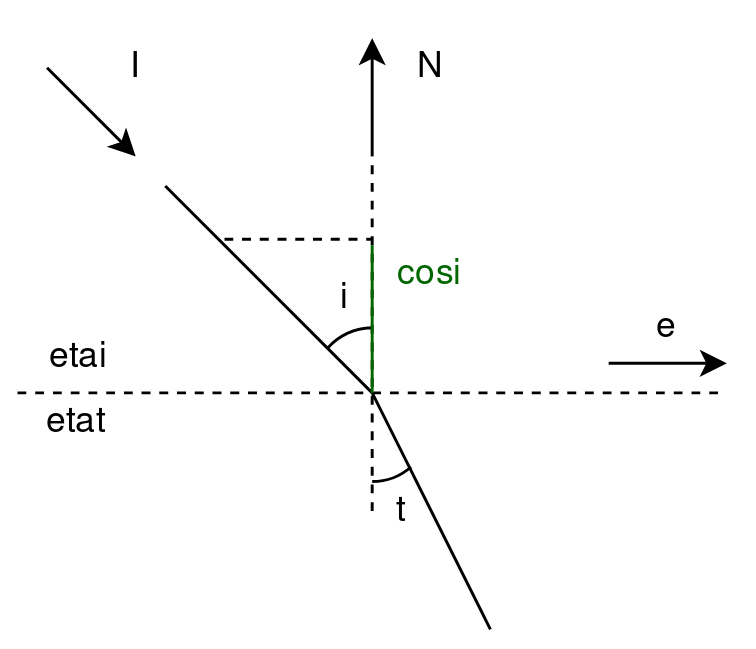
参考: t-pot『Ray Tracing : Reflection & Refraction』
屈折光の向きを表す単位ベクトルを$\vec{T}$、水平方向の単位ベクトルを$\vec{e}$とおく。
$$ \vec{T} = -\vec{N} \cos{t} + \vec{e} \sin{t} $$ $$ cosi = -(\vec{I} \cdot \vec{N}) $$
$\vec{e}\sin{i} = \vec{N}\cos{i} + \vec{I} = cosi\vec{N} + \vec{I}$より
$$ \begin{align} \vec{T} &= -\vec{N} \cos{t} + \frac{cosi\vec{N} + \vec{I}}{\sin{i}} \sin{t} \\\ &= -\vec{N} \cos{t} + \frac{\sin{t}}{\sin{i}} (cosi\vec{N} + \vec{I}) \end{align} $$
スネルの法則 $\frac{\sin{t}}{\sin{i}} = \frac{etai}{etat} = eta$ より
$$ \begin{align} \vec{T} &= -\vec{N} \cos{t} + eta (cosi\vec{N} + \vec{I}) \\\ &= -\vec{N} \sqrt{1 - \sin^2{t}} + eta (cosi\vec{N} + \vec{I}) \\\ &= -\vec{N} \sqrt{1 - eta^2 \sin^2{i}} + eta (cosi\vec{N} + \vec{I}) \\\ &= -\vec{N} \sqrt{1 - eta^2 (1-cosi^2)} + eta (cosi\vec{N} + \vec{I}) \\\ &= -\vec{N} \sqrt{k} + eta (cosi\vec{N} + \vec{I}) \\\ &= \vec{I} \times eta + \vec{N}(eta \times cosi - \sqrt{k}) \\\ \end{align} $$