最近そういうことをしたくなった。 情報系の大学で数学を勉強していればたぶん自力で作れるやつだが、ググると出てこないのでやり方を書いてみる。
逆関数法
どんな確率分布でも、その累積分布関数 ($F(x)$=出た値が$x$以下になる確率) の逆関数さえわかっていればその分布に従う確率変数を実現できる。 $[0,1)$ の一様分布に従う確率変数 $U$ を逆関数に渡してやるだけだ。
$$ X := F^{-1}(U) $$
これを最初に思いついた人は天才だと思う。
逆ガウス分布
というわけで累積分布関数の逆関数がわかっている任意の確率分布が生成できるようになった。 これを使って目的の乱数を作りたい。
待ち時間といえば待ち行列理論だ。 待ち行列理論でよく出てくる分布といえばポアソン分布等があるが、これは平均と分散が1つのパラメータで決まってしまう。 理論的な解析を行うときは計算が楽でいいが、分散や平均を自由に設定しようと思うと都合が悪い。
Wikipediaでいろんな確率分布を見てみると、逆ガウス分布というものが見つかった。
Inverse Gaussian distribution - Wikipedia
この分布には$\mu$と$\lambda$という2つのパラメータがあり、期待値(平均)は$\mu$、分散は$\mu^3/\lambda$になる。 そのため、$\mu$が0でないなら期待値と分散を自由に設定できる。 この分布の累積分布関数は以下のようになる。
$$ F(x) = \Phi\left(\sqrt{\frac{\lambda}{x}}\left(\frac{x}{\mu}-1\right)\right) + \rm{exp}\left(\frac{2\lambda}{\mu}\right)\Phi\left(-\sqrt{\frac{\lambda}{x}}\left(\frac{x}{\mu}+1\right)\right) $$
$$ \Phi(x) = \frac{1}{2}\left(1 + \rm{erf}\left(\frac{x}{\sqrt{2}}\right)\right) $$
$\rm{erf}(x)$はガウスの誤差関数というもので、数学のライブラリに入ってたりする。 Goの場合標準ライブラリに入っている。 一応これも書いておくと$\rm{exp}(x)=e^x$である。 複雑な累積分布関数で逆関数を求めるのは大変そうだが、累積分布関数は定義上単調増加なので二分法かなにかで近似したりすればいいと思う。
実装
というわけで実装してみる。まずは逆ガウス分布の累積分布関数inverseGaussianDistributionCDF。
func standardNormalDistributionCDF(x float64) float64 {
e := math.Erf(x / math.Sqrt(2))
return (1 + e) / 2
}
func inverseGaussianDistributionCDF(x float64, mu float64, lambda float64) float64 {
a := math.Sqrt(lambda/x) * ((x / mu) - 1)
b := math.Exp(2 * lambda / mu)
c := -math.Sqrt(lambda/x) * ((x / mu) + 1)
return standardNormalDistributionCDF(a) + b*standardNormalDistributionCDF(c)
}
次に、それを使って累積分布関数の逆関数を実装する。 二分法だけだと遅いのでニュートン法を使ってみたが、ときどきNaNが出てくるのを条件分岐で抑えているのでたぶんバグっている。
func (ig *InverseGaussianDistribution) InverseCDF(y float64) float64 {
if y <= 0 || 1 <= y {
return math.NaN()
}
// newton's method
x := 1.0
for i := 0; i < 50; i++ {
a := y - ig.CDF(x)
b := -ig.PDF(x)
if math.Abs(a/b) < 0.1 || math.IsInf(a/b, 0) || math.IsNaN(a/b) {
break
}
x = x - a/b
}
// bisection method
less := math.Max(0, x-0.25)
more := math.Max(0, x-0.25) + 0.5
for i := 0; i < 50; i++ {
m := less + (more-less)/2
if ig.CDF(m) < y {
less = m
} else {
more = m
}
}
return less
}
最後に、逆関数に一様乱数を渡せば完成。
func (ig *InverseGaussianDistribution) Float64() float64 {
return ig.InverseCDF(ig.rng.Float64())
}
コード全体はここに置いてある。一応ライブラリとして利用可能にしてある。
kotet/igaussian: Go library that provides Inverse Gaussian distributions
結果
$\mu=1, \lambda=3$で適当に1万回ほど生成してヒストグラムを作ってみる。
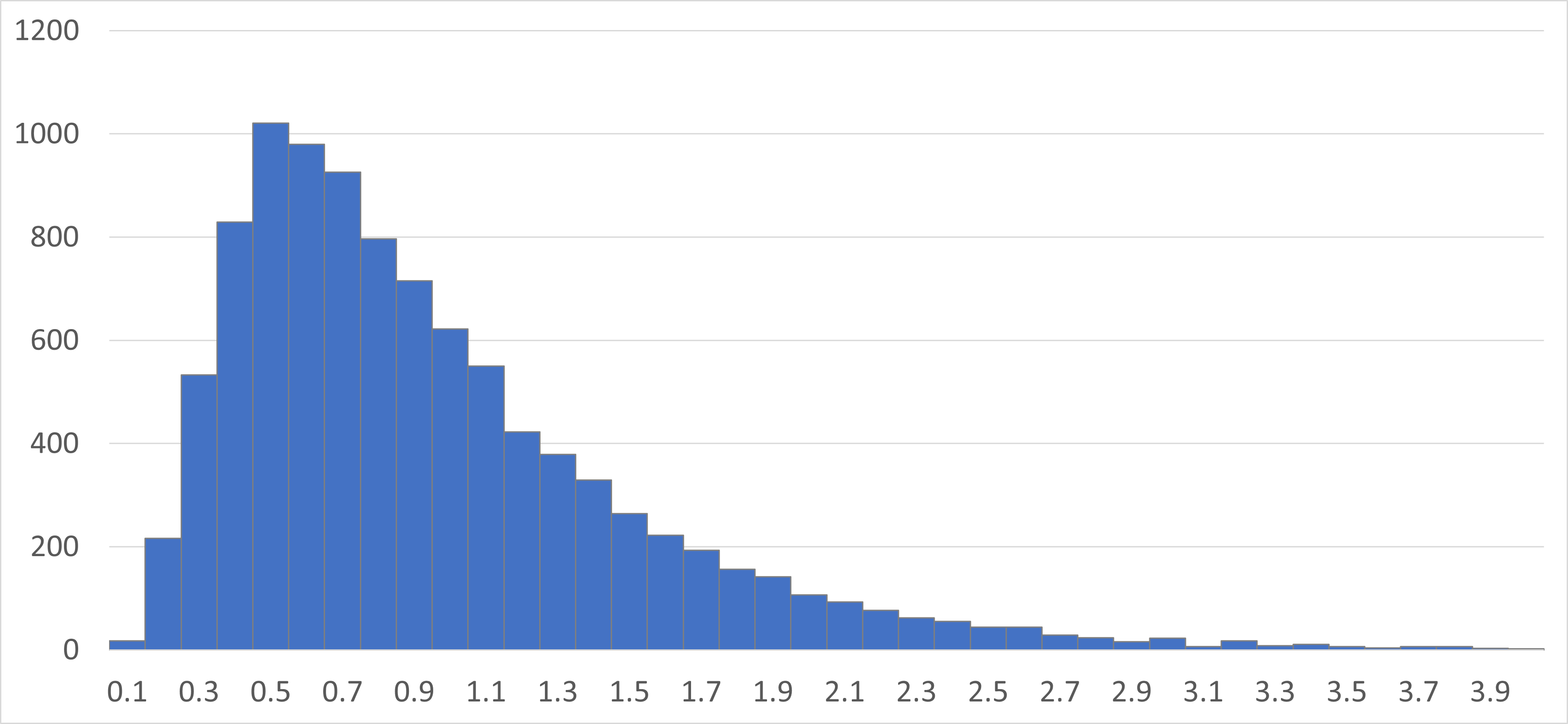
ここにきてようやく、実用上重要なのは期待値でなく最頻値ではないか? と思い至る。 期待値は$\mu$=1のはずだが、最頻値は0.5のあたりになっている。 最頻値の制御がしやすい分布を探すべきだろう。 探すべきだろうが力尽きたので、この話はここで終わる。