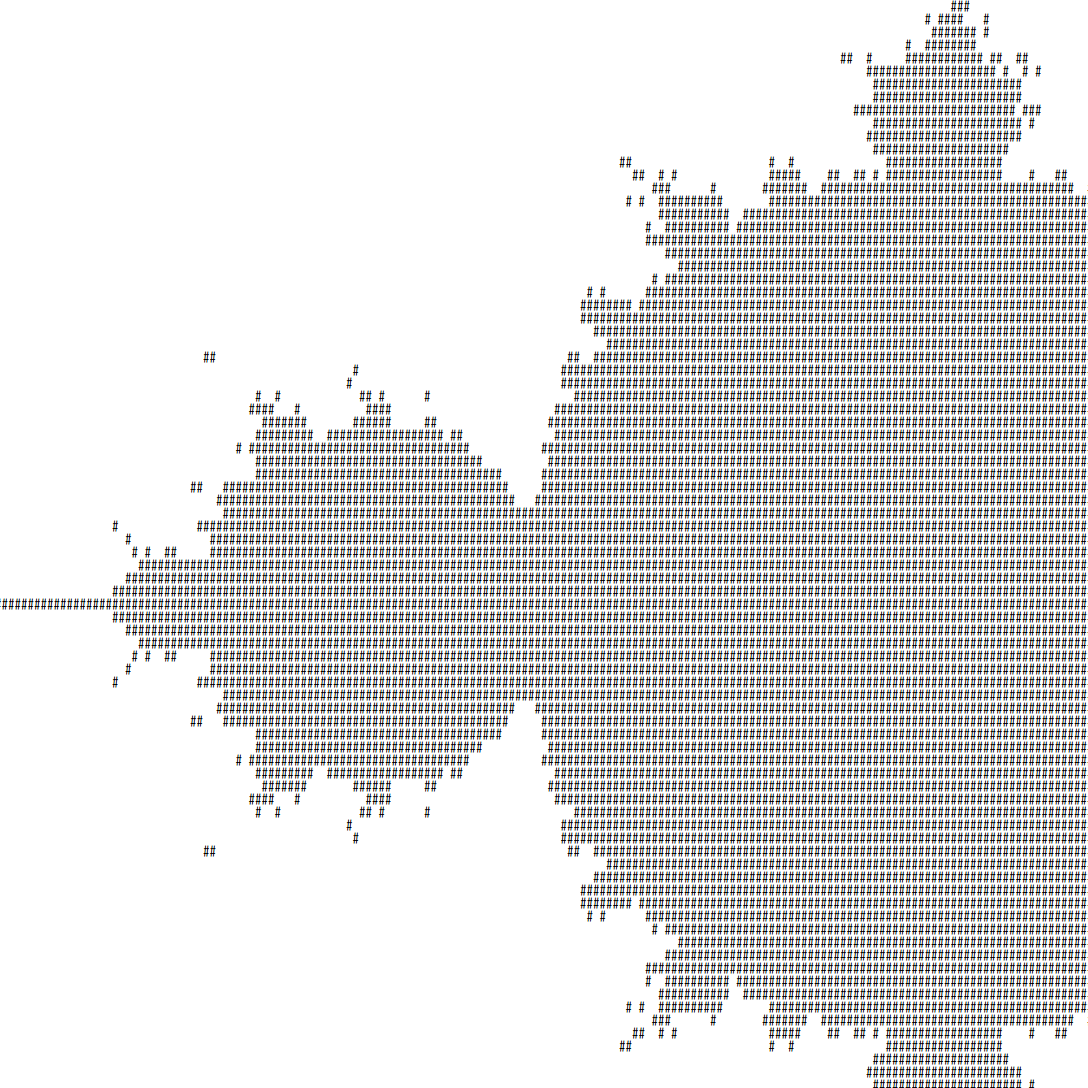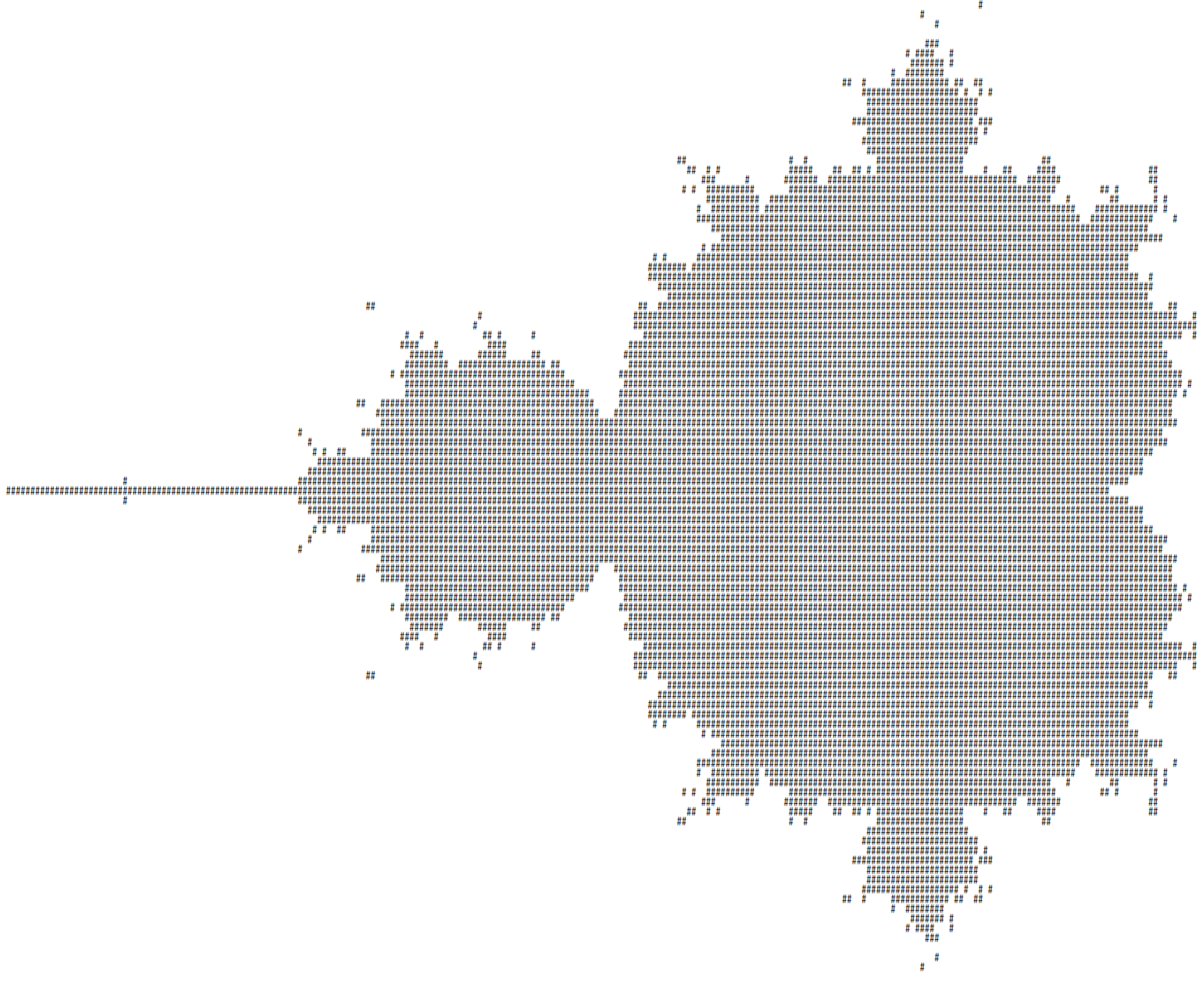
なにか計算的なことをやってみたくてマンデルブロ集合を書く。 「描く」ではなく「書く」なのはコマンドライン上に文字で表現するからである。
マンデルブロ集合とは
いろいろなサイトで出尽くしているけど一応書く。
\(z_{n+1}=z_n^2+c\) \(z_1=0\)
という漸化式が\(x \to \infty\)の極限で無限大に発散しない\(c\)の集合がマンデルブロ集合である。
つまり一つ一つ\(c\)を設定して発散しないか確かめて、それをプロットしていけばいい。
いろいろあって一度\(|z_n|>2\)になると発散するので、適当にnを増やしていって判定する。
一度も絶対値が2を超えなければ塗って、どこかで2を超えたら塗らない。
場合によっては発散したところにも2を始めに超えた時のnで色分けしたりする。
言語によっては実部と虚部を分けて実数計算に直したりするそうだが、Dにはstd.complexという複素数を表現できる
標準ライブラリがある。とてもつよい。
そういうわけでできたものがコチラである。dub run -- --row 100 --column 400で上の出力が得られる。
文字で表現する程度のサイズだと一瞬で終わってしまうので、次は画像、動画を生成したい。
import std.complex;
void main(string[] args)
{
import std.getopt : defaultGetoptPrinter, getopt, GetOptException,
GetoptResult;
import std.stdio : writeln;
real top = 1.0;
real left = -2.0;
real height = 2.0;
real width = 4.0;
size_t row = 20;
size_t column = 80;
size_t judge_iter = 20;
GetoptResult helpinfo;
try
{
helpinfo = getopt(args, "top", &top, "left", &left, "height",
&height, "width", &width, "row", &row, "column", &column,
"judge-iter", &judge_iter);
}
catch (Exception e)
{
writeln("Error: ", e.msg, "\nexit");
return;
}
if (helpinfo.helpWanted)
defaultGetoptPrinter("test", helpinfo.options);
draw(top, left, height, width, row, column, judge_iter).writeln;
}
string draw(real top, real left, real height, real width, size_t row,
size_t column, size_t judge_iter)
{
string result;
foreach (ro; 0 .. row)
{
foreach (co; 0 .. column)
{
// z(n+1) = z(n) ^ 2 + c; z(0) = 0
Complex!real c;
c.im = top - height * (cast(real) ro / row);
c.re = left + width * (cast(real) co / column);
if (isDiverge(c, judge_iter))
{
result ~= ' ';
}
else
{
result ~= '#';
}
}
result ~= '\n';
}
return result;
}
bool isDiverge(Complex!real c, size_t judge_iter)
{
auto z = complex!real(0, 0);
foreach (i; 0 .. judge_iter)
{
z = z * z + c;
if (2.0 < z.abs)
return true;
}
return false;
}